Intelligo
Simplifying Complexity
The asymptotic analysis of a given function is a means of finding the bounds of said function. As computer scientists, we are concerned with the complexity of a function because computers solve computational problems. By finding the complexities of our algorithms, we find the runtime of our programs. But what does this mean?$$O(n), \Omega(log(n)), \Omega(nlog(n)), \Theta(n^2)$$ If your tasked to find the worst-case runtime of an algorithm, what would you do? What about the best-case?
Not to worry! Once the terminology is clear, so are the steps. First things first, let us go over the input methods for the asymptotic complexity tool.
Usage Information
The following is a summay of how to input python math expressions, which is required to use the asymptotic complexity tool.
- Powers:$$n^i \longrightarrow n**i$$
- Multiplication:$$nc \longrightarrow n*i$$
- Division:$$\frac{n}{c} \longrightarrow n/c$$
- Logarithms:$$logn \longrightarrow log(n)$$
- Addition & Subtraction:$$n + a - b \longrightarrow n + a - b$$
Now that that's out of the way, let's move on to the interesting stuff.
Using Limits to Bound a Function
This method is quite simple. Given the function you are analyzing, f(n) we divide by some other function, g(n). All we must find is the limit of this quotient as n approaches infinity. The beauty is we can choose any function g(n), no pressure. Preferably, we would choose g(n) to be as tight a bound as possible... but you can also pick right out of a hat. Have a little fun with it. $$\text{Given functions: } f(n) \text{ and } g(n)$$ $$\lim_{n \rightarrow \infty} \frac{f(n)}{g(n)} \rightarrow \textbf{ some answer we care about }$$ Why do we care about this answer? Espesically, if g(n) can be anything. Well, based on the answer we find we can say something about the relationship between these two functions.
If the limit as n grows to infinity is 0, we know from our solid maths skills the numerator grows slower than
the denominator.
Which implies we have found an upper bound to f(n).
Similarly, if the limit as n grows to infinity is infinity. Then we know the numerator grows faster than the
denominator.
Which implies we have found a lower bound to f(n).
The following table shows details on all the notational terms common in the field asymptotic complexity.
| Notation | Name | Bound | Limit |
|---|---|---|---|
| $$f(n) \in o(g(n))$$ | Little Oh | $$f < g \therefore \text{ g(n) is an upper bound}$$ | $$\lim_{n \rightarrow \infty} \frac{f(n)}{g(n)} = 0$$ |
| $$f(n) \in O(g(n))$$ | Big Oh | $$f \leq g \therefore \text{ g(n) is an upper bound}$$ | $$\lim_{n \rightarrow \infty} \frac{f(n)}{g(n)} \in [0, \infty)$$ |
| $$f(n) \in \omega(g(n))$$ | Little Omega | $$f > g \therefore \text{ g(n) is an lower bound}$$ | $$\lim_{n \rightarrow \infty} \frac{f(n)}{g(n)} = \infty$$ |
| $$f(n) \in \Omega(g(n))$$ | Big Omega | $$f \geq g \therefore \text{ g(n) is an upper bound}$$ | $$\lim_{n \rightarrow \infty} \frac{f(n)}{g(n)} \in (0, \infty]$$ |
| $$f(n) \in \Theta(g(n))$$ | Theta | $$f = g \therefore \text{ g(n) is an tight bound}$$ | $$\lim_{n \rightarrow \infty} \frac{f(n)}{g(n)} \in (0, \infty)$$ |
Generalized Graphs of Asymptotic Notations
Number of operations versus input size for example functions
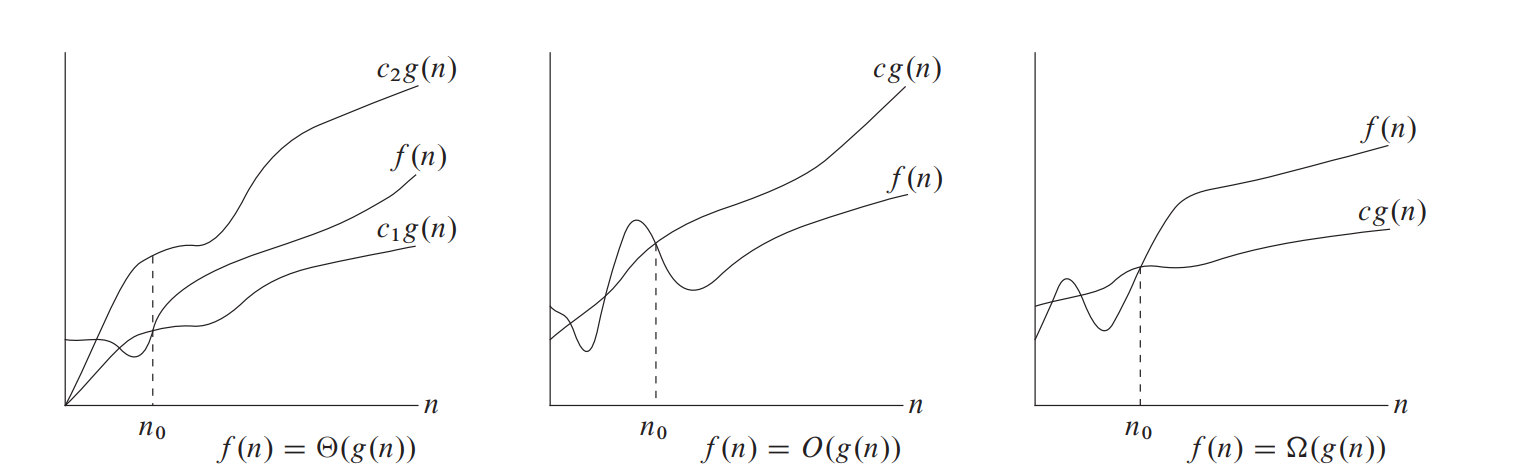
Big Theta is shown as a tight bound.
Big Oh is shown as a upper bound.
Big Omega is shown as a lower bound.
Disclaimer: These graphs are not based on user input. They are examples to aid in visualizing the meaning of Big Oh, Theta, and Omega.
Cormen, T.H., et al. Introduction to Algorithms. MIT Press, 2009. Page 45.
Mastering Master's
The Master's Method, also known as the Master's Theorem, is a simple way to solve recurrences of the following form, $$ T(n)=aT(\frac{n}{b})+ \Theta(f(n))$$ More specifically, $$T(n)=aT(\frac{n}{b})+ \Theta(n^{k}(log^{i}n))$$ $$a \rightarrow \text{number of subproblems in recurrence relation}$$ $$b \rightarrow \text{branching factor which reduces the subproblem with each recursive call}$$ $$\text{Base Case} \rightarrow T(0) = \Theta(1)$$
Moreover, the following variable must be defined using variables a and b, $$c_{critical} = \textit{the work to split/recombine vs subproblems}$$ $$= \textit{log(# of subproblems)/log(relative problem size)}$$ $$= log(a)/log(b)$$ $$= log_{b} a $$
This method can be used to solve all recurrences which adhere to the following rules:
- a must be be at least 0
- b must be an integer larger than 1
- k must be at least 0
- i must be at least 0
- All argument values must be constants
- Must have polynomial difference between, $$f(n) \text{ and } n^{\log _{b} a}$$
If each of these criteria is met, you may then solve your recurrence with the Master's Method! So what is this method, you ask? The following table is a summary of what the theorem states,
| Case | Condition | Master's Theorem bound |
|---|---|---|
| 1 | $$f(n) = O(n^c) \textit{ such that } c < c_{critical}$$ | $$T(n) = \Theta(n^{c_{critical}})$$ |
| 2 | $$f(n) = \Theta(n^{c_{critical}} log^{i} n)$$ | $$T(n) = \Theta(n^{c_{critical}} log^{i+1} n)$$ |
| 3 | $$ f(n) = \Omega(n^c) \textit{ such that } c > c_{critical}$$ | $$T(n) = \Theta(f(n))$$ |